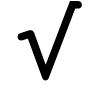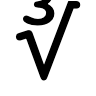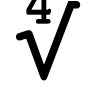রেডিক্যাল চিহ্ন

	HTML	মিনিং
√	√ √ U+221A	বর্গমূল চিহ্ন বর্গমূল চিহ্ন (√) হল নির্দেশ করে একটি সংখ্যার বর্গমূল।
∛	∛ U+221B	ঘাতমূল চিহ্ন ঘাতমূল চিহ্ন (∛) হল একটি সংখ্যার ঘাতমূল।
∜	∜ U+221C	চতুর্থ মূল চিহ্ন চতুর্থ মূল চিহ্ন (∜) হল একটি সংখ্যার চতুর্থ মূল।
²	² ² U+B2	বর্গ চিহ্ন একটি সংখ্যার বর্গ চিহ্ন বোঝানোর জন্য ব্যবহৃত হয়।
³	³ ³ U+B3	ঘাত চিহ্ন একটি সংখ্যার ঘাত চিহ্ন বোঝানোর জন্য ব্যবহৃত হয়।
⁴	⁴ U+2074	চতুর্থ ঘাত চিহ্ন একটি সংখ্যার চতুর্থ ঘাত চিহ্ন বোঝানোর জন্য ব্যবহৃত হয়।
±	± ± U+B1	প্লাস-মাইনাস চিহ্ন একটি সংখ্যার ধনাত্মক এবং ঋণাত্মক বর্গমূলগুলি প্রতীক্ষালাভ করে।

রেডিক্যাল চিহ্ন কি?

রেডিক্যাল চিহ্নটি বর্গমূল বা n-তম মূল নির্দেশ করতে ব্যবহৃত হয়। এটি বিভিন্ন রূপে পাওয়া যায়, যেমন বর্গমূলের জন্য √, ঘাতমূলের জন্য ∛ এবং চতুর্থ মূলের জন্য ∜। এগুলি বীজগণিত, ক্যালকুলাস, এবং বিভিন্ন অন্যান্য গণিতবিদ্যার মৌলিক ধারণার চিহ্ন।

রেডিক্যাল চিহ্নের পরিবর্তনশীলতা

রেডিক্যাল চিহ্নটি বিভিন্ন রূপে আসে, যেমন বর্গমূলের জন্য (√), ঘাতমূলের জন্য (∛) এবং চতুর্থ মূলের জন্য (∜)। মনে রাখবেন যে বর্গমূল চিহ্ন (√) পরিবর্তনশীলতা করার জন্য উপপাদক 2 প্রয়োজন নেই, যদিও অন্যান্য মূল চিহ্নগুলি যথাযথ উপপাদকগুলি (³, ⁴) দরকার পায় স্পষ্টতার জন্য।

রেডিক্যাল চিহ্নের বিভিন্ন ক্ষেত্রে ব্যবহার

রেডিক্যাল চিহ্নটি বিভিন্ন বিষয়গুলিতে ব্যবহৃত হয়:

• গণিত: বীজগণিত, ক্যালকুলাস, এবং ট্রাইগোনোমেট্রিতে ব্যাপকভাবে ব্যবহৃত।
• কম্পিউটার বিজ্ঞান: দূরত্ব গণনার জন্য এবং বিভিন্ন অপটিমাইজেশন সমস্যাগুলিতে ব্যবহৃত হয়।
• ইঞ্জিনিয়ারিং: স্ট্রেস এবং স্ট্রেন প্রকারণের মতামত পরিকল্পনা করার জন্য ব্যবহৃত হয়।
• পদার্থবিদ্যা: শক্তি, গতি এবং তরঙ্গ সংক্রান্ত সমীকরণগুলিতে ব্যবহৃত হয়।

কীবোর্ড শর্টকাট, অ্যাল্ট কোড এবং লাটেক্স ব্যবহার করে রেডিক্যাল চিহ্ন টাইপ করার পদ্ধতি

• Windows: Alt কী ধরে রাখুন এবং সংখ্যারিক কীপ্যাডে লিখুন 251 এবং পরে Alt কী মুক্ত করুন এইভাবে √ চিহ্নটি পান।
• Mac: √ চিহ্নের জন্য Option + v চাপুন।
• Linux: Ctrl + Shift + u চাপুন, তারপর 221A টাইপ করুন এবং Enter চাপুন √ চিহ্নটি পান।
• HTML: √ চিহ্নের জন্য নেমড এন্টিটি √ বা নিউমেরিক এন্টিটি √ ব্যবহার করুন।
• লাটেক্স: বর্গমূলের জন্য লাটেক্সে টাইপ করতে \sqrt{} কমানটি ব্যবহার করুন এবং n-তম মূলের জন্য \sqrt[n]{} কমানটি ব্যবহার করুন।

প্রতীকের চিত্র